Numerical Method for Linear equations

Numerical Method for Linear equations

重要

Consider the time-dependent Cauchy probelm of scalar equation,

$$\begin{equation} \left\{ \begin{array}{lr} u_t + au_x = 0, \qquad -\infty < x < \infty, t \geq 0 \\ u(x,0) = u_0(x) \end{array} \right. \end{equation}$$

Define:

• $h = \Delta x$
• $k = \Delta t$
• $x_j = jh, j = \cdots,-1,0,1,\cdots$
• $t_n = nk, n = 0,1,2,\cdots$
• $x_{j+\frac{1}{2}} = x_j + h/2 = (j+\frac{1}{2})h$
• $\lambda = \frac{k}{h}$

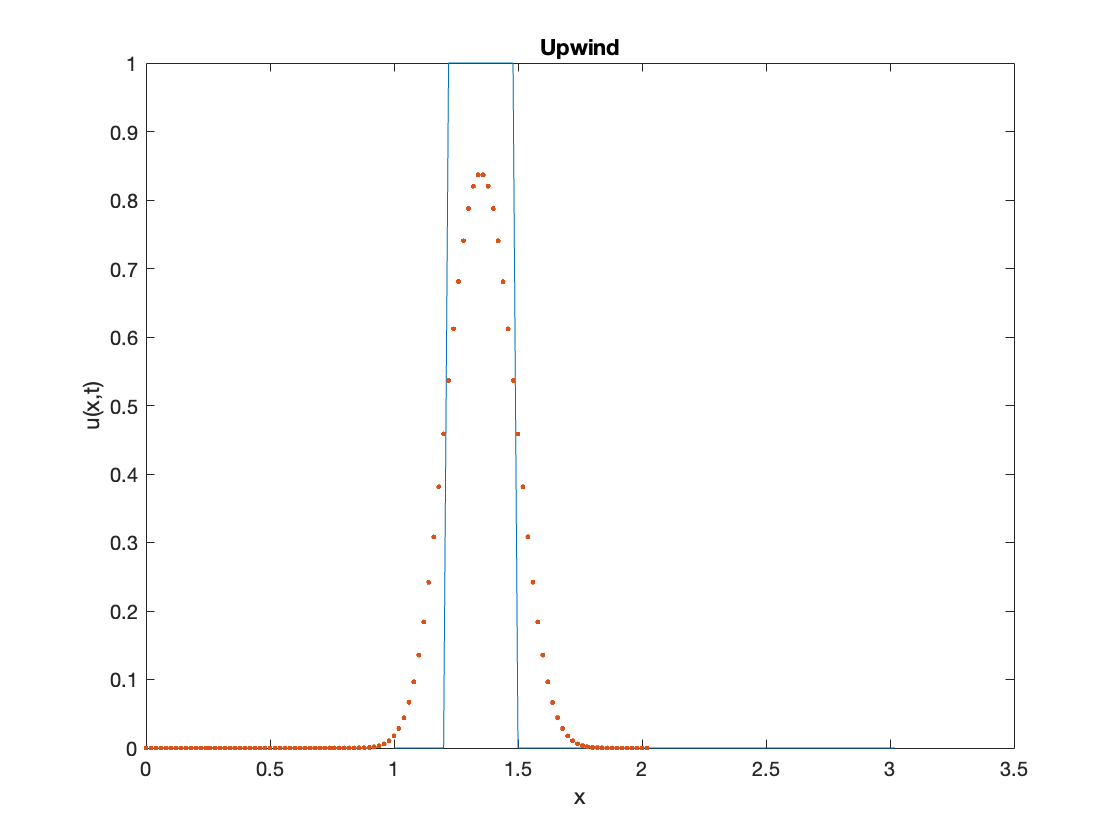
Up-Wind schemes:

$$\begin{equation} u_{j}^{n+1} = u_{j}^{n} - \frac{\lambda}{2}a(u_{j+1}^{n} - u_{j-1}^{n}) + \frac{\lambda}{2}|a|(u_{j+1}^{n} - 2u_{j}^{n} + u_{j-1}^{n}) \end{equation}$$

subroutine core_algorithmn_upwind
    
    implicit none
    integer :: i
    
    t1_vertex(0)%value = t0_vertex(0)%value - lambda * 0.5 * ax(x(0)) * (t0_vertex(1)%value - t0_vertex(nx)%value) + lambda * 0.5 * abs(ax(x(0))) * (t0_vertex(1)%value - 2. * t0_vertex(0)%value  + t0_vertex(nx)%value)
    t1_vertex(nx)%value = t0_vertex(nx)%value - lambda * 0.5 * ax(x(0)) * (t0_vertex(0)%value - t0_vertex(nx-1)%value) + lambda * 0.5 * abs(ax(x(0))) * (t0_vertex(0)%value - 2. * t0_vertex(nx)%value + t0_vertex(nx-1)%value)
    do i = 1,nx
        
        t1_vertex(i)%value = t0_vertex(i)%value - lambda * 0.5 * ax(x(i)) * (t0_vertex(i+1)%value - t0_vertex(i-1)%value) + lambda * 0.5 * abs(ax(x(i))) * (t0_vertex(i+1)%value - 2. * t0_vertex(i)%value  + t0_vertex(i-1)%value)
    
    enddo
    
    do i = 1 - nghost, nx + nghost
        
        t0_vertex(i)%value = t1_vertex(i)%value
    
    enddo
    
end subroutine core_algorithmn_upwind

UpWind method

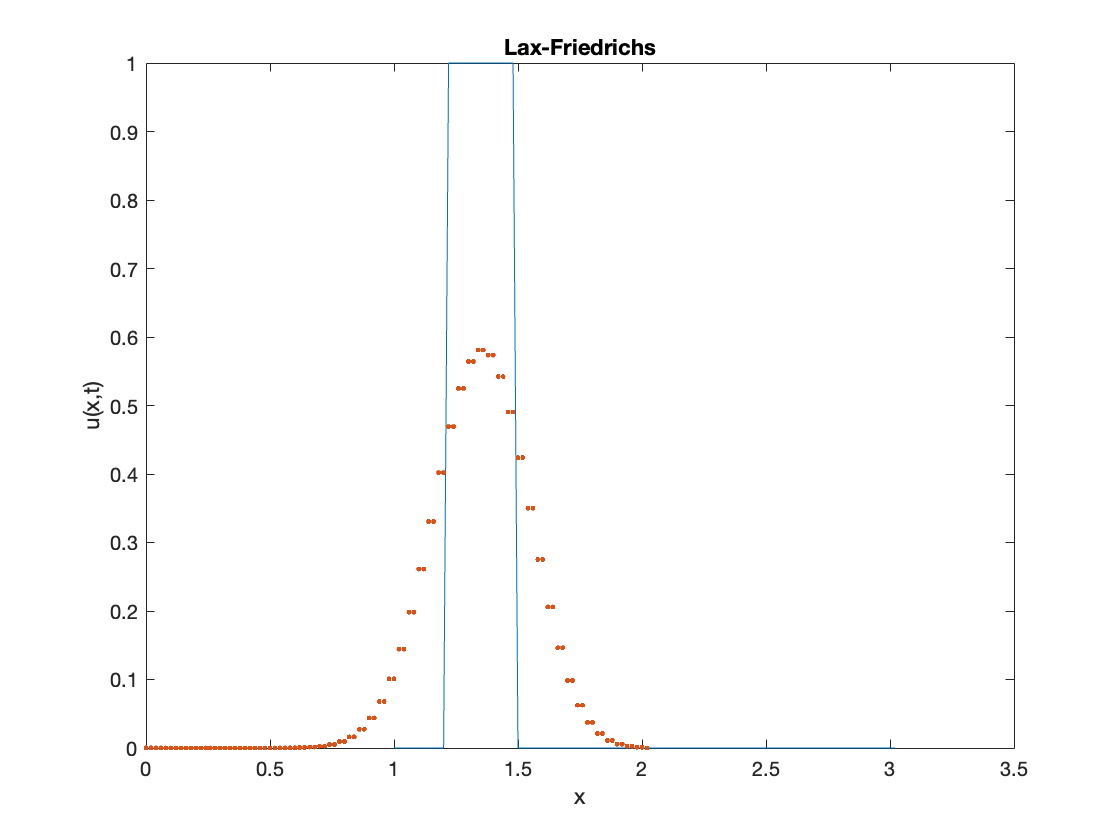
Lax-Friedrichs

$$\begin{equation} u_{j}^{n+1} = u_{j}^{n} - \frac{\lambda}{2}a(u_{j+1}^{n} - u_{j-1}^{n}) + \frac{1}{2}(u_{j+1}^{n} - 2u_{j}^{n} + u_{j-1}^{n}) \end{equation}$$

subroutine core_alogrithmn_LaxFriedrichs
    implicit none
    integer :: i
    
    t1_vertex(0)%value = t0_vertex(0)%value - lambda * 0.5 * ax(x(0)) * (t0_vertex(1)%value - t0_vertex(nx)%value) + 0.5 * (t0_vertex(1)%value - 2. * t0_vertex(0)%value  + t0_vertex(nx)%value)
    t1_vertex(nx)%value = t0_vertex(nx)%value - lambda * 0.5 * ax(x(nx)) * (t0_vertex(0)%value - t0_vertex(nx-1)%value) + 0.5 * (t0_vertex(0)%value - 2. * t0_vertex(nx)%value + t0_vertex(nx-1)%value)
    do i = 1,nx
        
        t1_vertex(i)%value = t0_vertex(i)%value - lambda * 0.5 * ax(x(i)) * (t0_vertex(i+1)%value - t0_vertex(i-1)%value) + 0.5 * (t0_vertex(i+1)%value - 2. * t0_vertex(i)%value  + t0_vertex(i-1)%value)
    
    enddo
    
    do i = 1 - nghost, nx + nghost
        
        t0_vertex(i)%value = t1_vertex(i)%value
    
    enddo

end subroutine core_alogrithmn_LaxFriedrichs

Lax-Friedrichs

Lax-Friedrichs (Local)

In this case, the pde equation that we want to solve the Burgers' equation is

$$\begin{equation} u_t + (\frac{1}{2}u^2)_x = 0 \end{equation}$$

with the initial solution is

$$\begin{equation} u(x,0) = 0.5 + \sin(\pi x) \end{equation}$$

The Lax-Friednrichs will be changed into

$$\begin{equation} u_{j}^{n+1} = u_{j}^{n} + \frac{\Delta t}{\Delta x}[\hat{f}_{j+\frac{1}{2}}(u_j,u_{j+1})-\hat{f}_{j-\frac{1}{2}}(u_{j-1},u_j)] \end{equation}$$

where

$$\begin{equation} \hat{f}_{j+\frac{1}{2}}(u_j,u_{j+1}) = \frac{1}{2}[(f(u_j) + f(u_{j+1})) - \alpha(u_{j+1}-u_j)] \end{equation}$$

with

$$\begin{equation} \alpha = \max_{u\in(u_{j-1},u_{j})}{f^{'}(u)} \end{equation}$$

$$\begin{equation} \hat{f}_{j-\frac{1}{2}}(u_{j-1},u_{j}) = \frac{1}{2}[(f(u_{j-1}) + f(u_{j})) - \alpha(u_{j}-u_{j-1})] \end{equation}$$

with

$$\begin{equation} \alpha = \max_{u\in(u_{j},u_{j+1})}{f^{'}(u)} \end{equation}$$

where $f(u) = \frac{1}{2}u^2$

Therefore, the final result is:

$$\begin{equation} u_{j}^{n+1} = u_{j}^{n} + \frac{\Delta x}{\Delta t}[\frac{1}{4}(u^{2}_{j+1} - u^{2}_{j-1}) + \max\{u_{j-1},u_{j}\}\cdot(u_j - u_{j-1}) - \max\{u_{j},u_{j+1}\}\cdot(u_{j+1} - u_{j})] \end{equation}$$

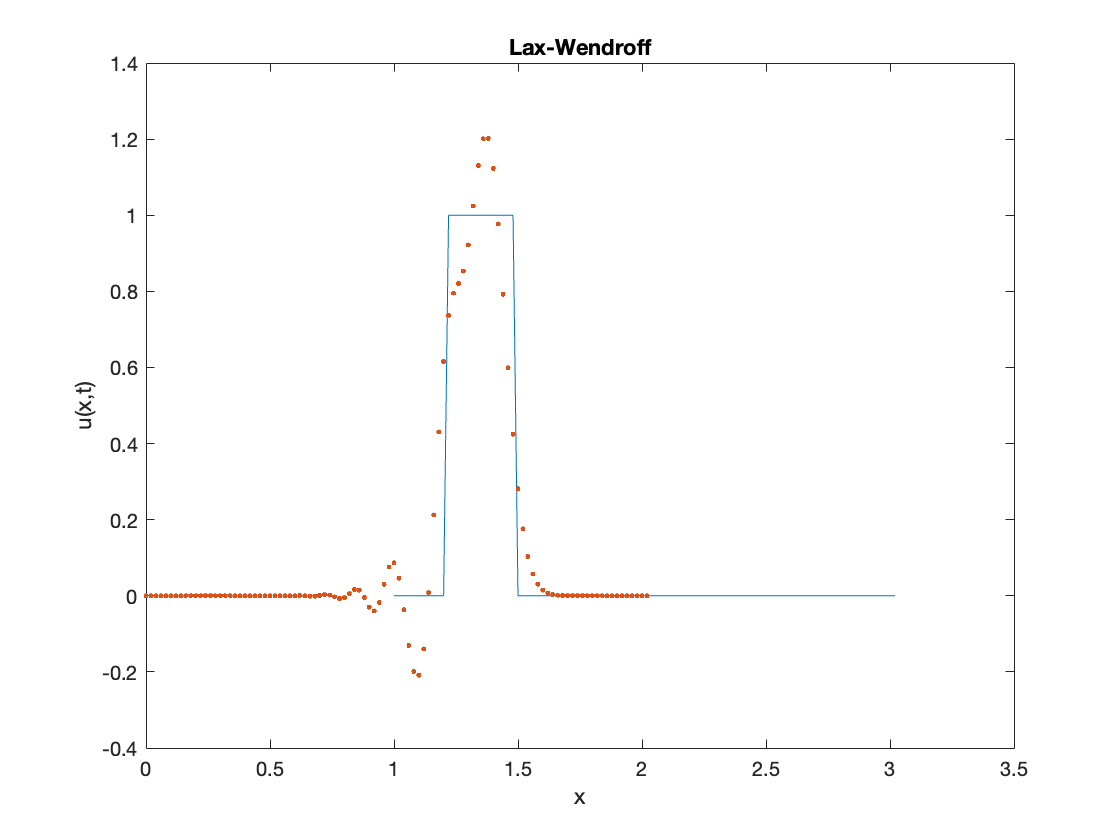
Lax-Wendroff

The general form:

$$\begin{equation} u_{j}^{n+1} = \frac{\lambda + \lambda^2}{2}u_{j-1}^n + (1-\lambda^2)u_j^{n} + \frac{\lambda^2-\lambda}{2}u_{j+1}^n \end{equation}$$

After the expansion:

$$\begin{equation} u_{j}^{n+1} = u_{j}^{n} - \frac{\lambda}{2}a(u_{j+1}^{n} - u_{j-1}^{n}) + \frac{1}{2}(u_{j+1}^{n} - 2u_{j}^{n} + u_{j-1}^{n}) \end{equation}$$

subroutine core_alogrithmn_LaxWendroff
    implicit none
    integer :: i
    
    t1_vertex(0)%value = t0_vertex(0)%value - lambda * 0.5 * ax(x(0)) * (t0_vertex(1)%value - t0_vertex(nx)%value) + lambda ** 2 * 0.5 * ax(x(0)) ** 2 * (t0_vertex(1)%value - 2 * t0_vertex(0)%value + t0_vertex(nx)%value)
    t1_vertex(nx)%value = t0_vertex(nx)%value - lambda * 0.5 * ax(x(nx)) * (t0_vertex(0)%value - t0_vertex(nx-1)%value) + lambda ** 2 * 0.5 * ax(x(nx)) ** 2 * (t0_vertex(0)%value - 2 * t0_vertex(nx)%value + t0_vertex(nx-1)%value)

    do i = 1,nx
        
        t1_vertex(i)%value = t0_vertex(i)%value - lambda * 0.5 * ax(x(i)) * (t0_vertex(i+1)%value - t0_vertex(i-1)%value) + lambda ** 2 * 0.5 * ax(x(i)) ** 2 * (t0_vertex(i+1)%value - 2 * t0_vertex(i)%value + t0_vertex(i-1)%value)
    
    enddo
    
    do i = 1 - nghost, nx + nghost
        
        t0_vertex(i)%value = t1_vertex(i)%value
    
    enddo

end subroutine core_alogrithmn_LaxWendroff

Lax-Wendroff

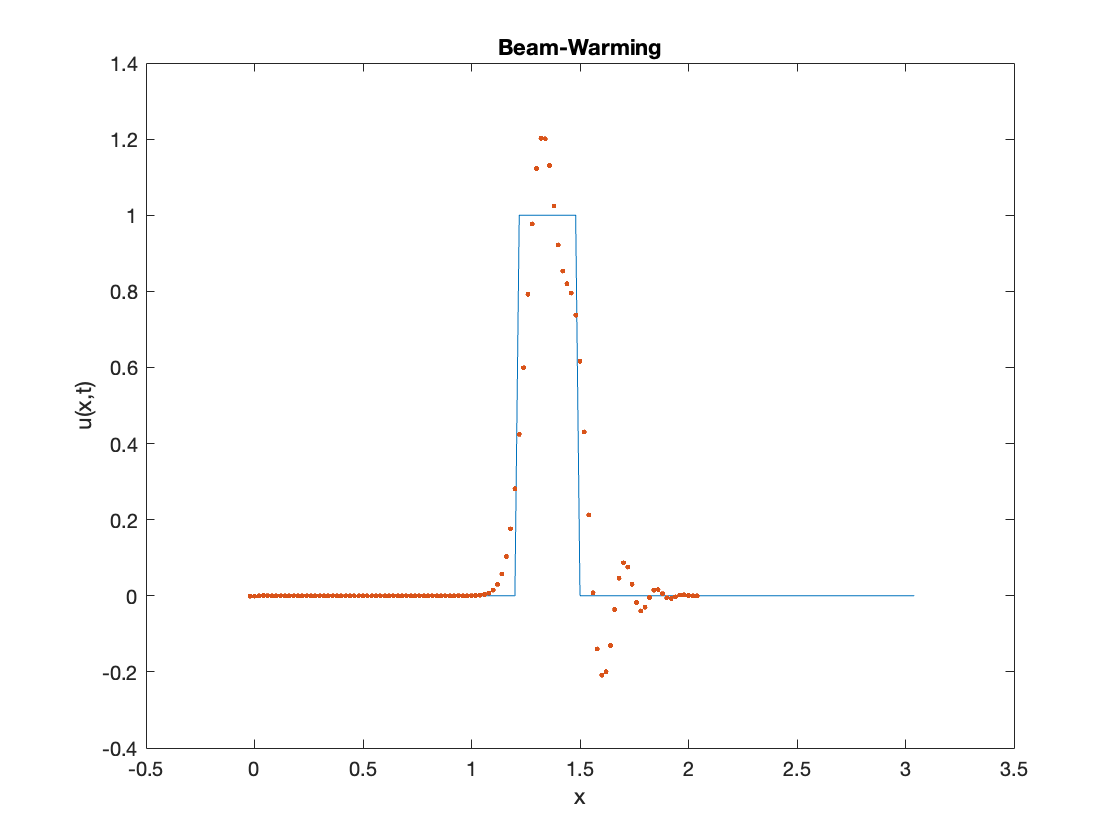
Beam-Warming

The general form:

$$\begin{equation} u_{j}^{n+1} = \frac{\lambda^2 - \lambda}{2}u_{j-2}^n + \lambda(2-\lambda)u_{j-1}^{n} + \frac{(1-\lambda)(2-\lambda)}{2}u_{j}^n \end{equation}$$

subroutine core_algorithmn_BeamWarming
    implicit none
    integer :: i
    
    t1_vertex(1 - nghost)%value = (lambda ** 2 - lambda) * 0.5 * t0_vertex(nx-1)%value + lambda * (2 - lambda) * t0_vertex(nx)%value + (1 - lambda) * (2 - lambda) * 0.5 * t0_vertex(1 - nghost)%value
    t1_vertex(0)%value = (lambda ** 2 - lambda) * 0.5 * t0_vertex(nx)%value + lambda * (2 - lambda) * t0_vertex(1 - nghost)%value + (1 - lambda) * (2 - lambda) * 0.5 * t0_vertex(0)%value

    do i = 1, nx
        t1_vertex(i)%value = (lambda ** 2 - lambda) * 0.5 * t0_vertex(i-2)%value + lambda * (2 - lambda) * t0_vertex(i-1)%value + (1 - lambda) * (2 - lambda) * 0.5 * t0_vertex(i)%value
    enddo
    
    do i = 1 - nghost, nx + nghost
        
        t0_vertex(i)%value = t1_vertex(i)%value
    
    enddo

end subroutine core_algorithmn_BeamWarming

Beam Warming