Definition 2.1
Let G be a graph with n vertices, the Laplacian matrix of G is an n×n matrix L(G)=(lij)n×n defined as:
lij:=⎩⎨⎧deg(vi), if i=j−1, if i=j and vi is adjacent tovj0, otherwise
Similarly, L(G) is a symmetric matrix. And,
L(G)=D(G)−A(G)
where D(G) is the degree matrix(对角线上全是 degree,别的地方都是 0 的矩阵) whose diagonal entries are deg(vi). A(G) is the adjacency matrix.
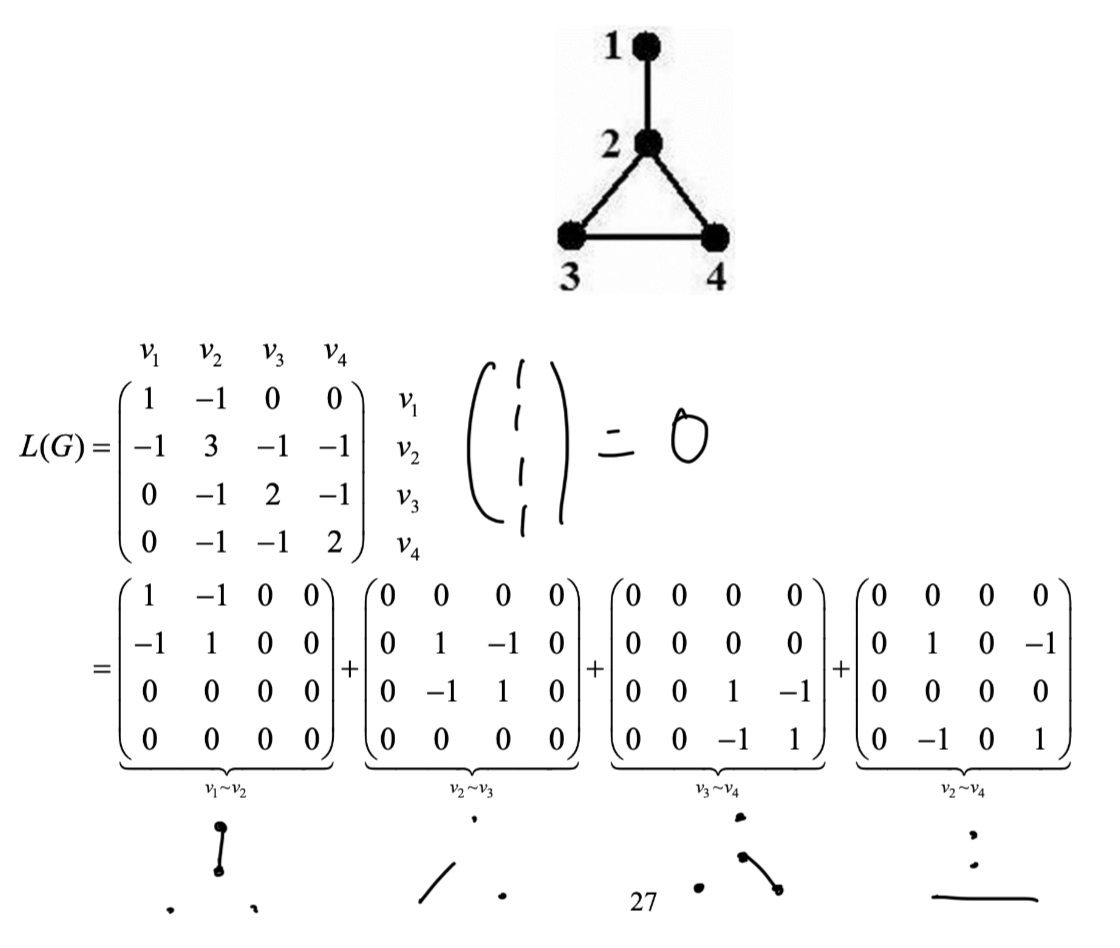 Example 2.2
Example 2.2