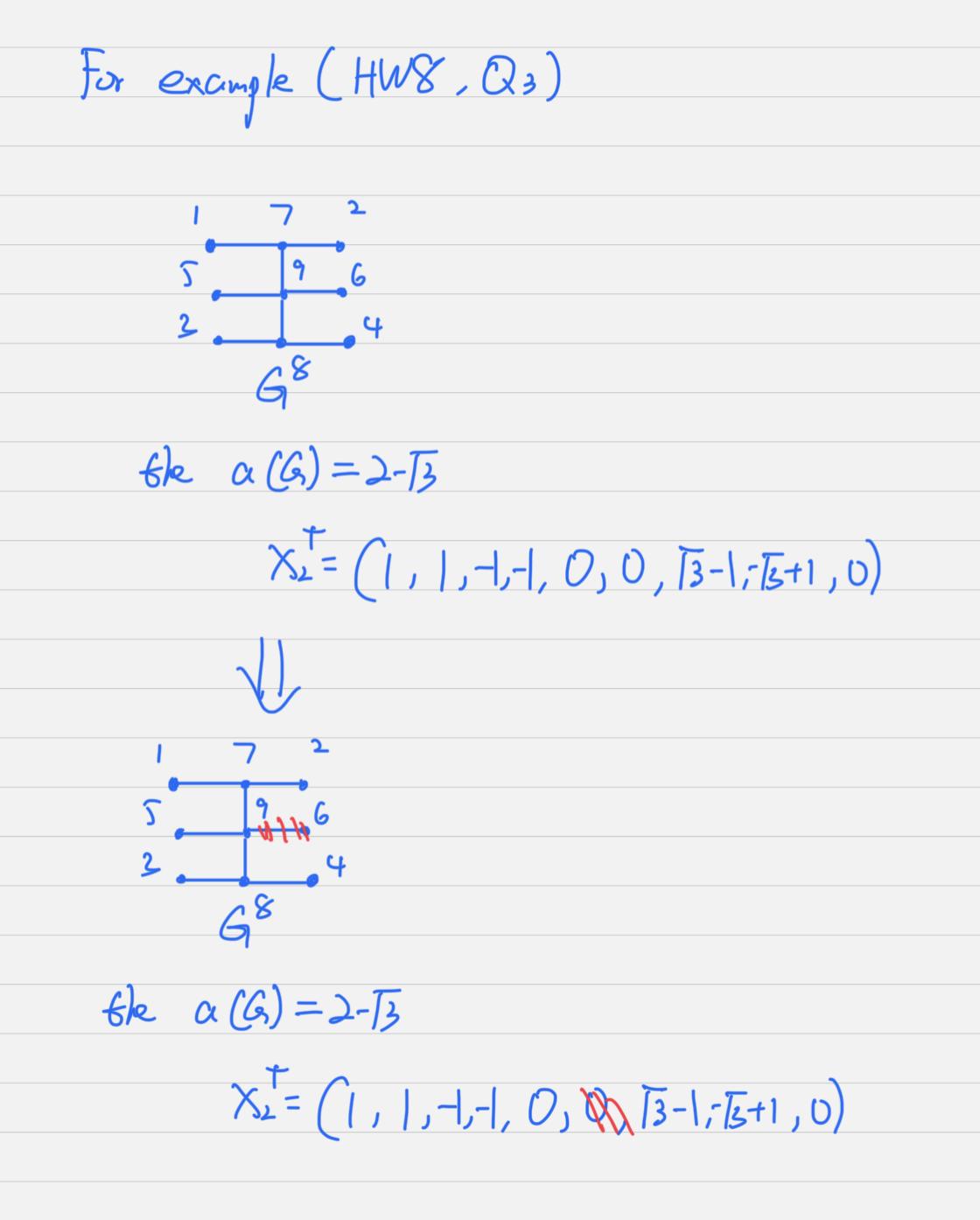IMPORTANT
The algebraic connectivity of G G G λ 2 ( G ) \lambda_2(G) λ 2 ( G ) L ( G ) L(G) L ( G ) G G G a ( G ) a(G) a ( G )
λ 2 ( G ) = a ( G ) \lambda_2(G) = a(G) λ 2 ( G ) = a ( G ) λ 2 ( G ) \lambda_2(G) λ 2 ( G ) IMPORTANT
If G 1 , G 2 G_1, G_2 G 1 , G 2 edge-disjoint grpah with the same set of vertices then
a ( G 1 ) + a ( G 2 ) ≤ a ( G 1 ∪ G 2 ) \begin{equation} a(G_1) + a(G_2) \leq a(G_1 \cup G_2) \end{equation} a ( G 1 ) + a ( G 2 ) ≤ a ( G 1 ∪ G 2 )
Corollargy
The function a ( G ) a(G) a ( G )
E ( G 1 ) ⊆ E ( G 2 ) and V ( G 1 ) = V ( G 2 ) \begin{equation} E(G_1) \subseteq E(G_2) \text{ and } V(G_1) = V(G_2) \end{equation} E ( G 1 ) ⊆ E ( G 2 ) and V ( G 1 ) = V ( G 2 )
Then,
a ( G 1 ) ≤ a ( G 2 ) \begin{equation} a(G_1) \leq a(G_2) \end{equation} a ( G 1 ) ≤ a ( G 2 )
Example:
G ⊂ K n − e ⇒ G is the subgraph of K n − e ⇓ a ( G ) ≤ a ( K n − e ) \begin{equation} \begin{array}{lr} G \subset K_n - e & \Rightarrow \text{G is the subgraph of } K_n-e \\ \qquad \Downarrow &\\ a(G) \leq a(K_n - e) & \end{array} \end{equation} G ⊂ K n − e ⇓ a ( G ) ≤ a ( K n − e ) ⇒ G is the subgraph of K n − e
IMPORTANT
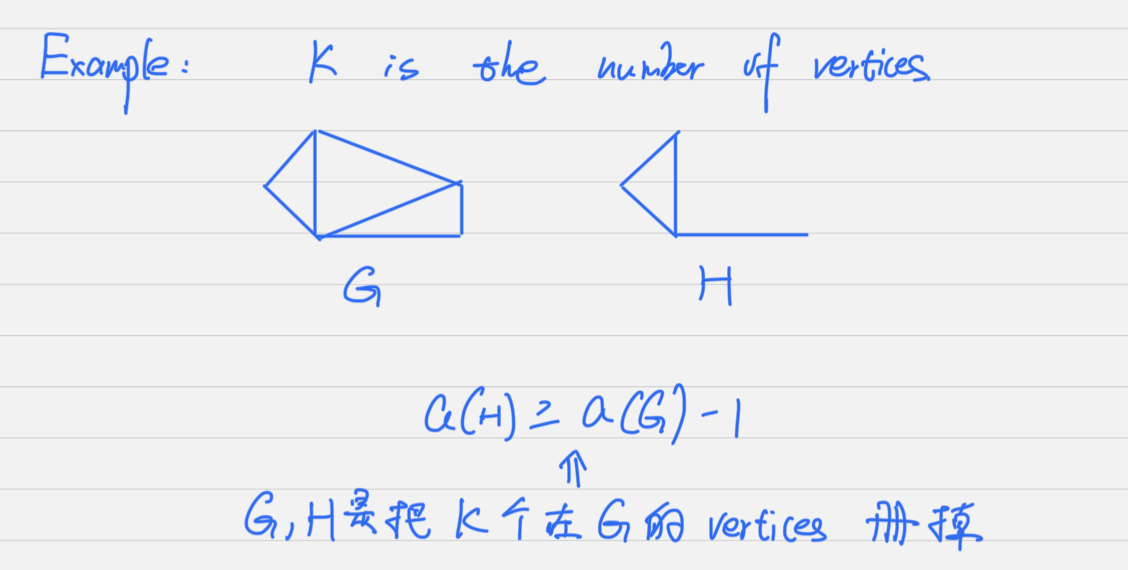
Let G G G H H H K K K G G G
Then,
a ( H ) ≥ a ( G ) − K \begin{equation} a(H) \geq a(G) - K \end{equation} a ( H ) ≥ a ( G ) − K
Corollary
Let G be a graph with vertex set V ( G ) V(G) V ( G ) V ( G ) = V 1 ∪ V 2 V(G) = V_1 \cup V_2 V ( G ) = V 1 ∪ V 2
For i = 1 , 2 i = 1,2 i = 1 , 2 G i G_i G i V i V_i V i
a ( G ) ≤ min { a ( G 1 ) + ∣ V 2 ∣ , a ( G ) + ∣ V 1 ∣ } ⇐ 两个图拆开后的结论 \begin{equation} a(G) \leq \min\{a(G_1) + |V_2|, a(G)+|V_1|\} \Leftarrow \text{ 两个图拆开后的结论} \end{equation} a ( G ) ≤ min { a ( G 1 ) + ∣ V 2 ∣ , a ( G ) + ∣ V 1 ∣ } ⇐ 两个图拆开后的结论
Definition
A connected graph G G G v v v cut vertex of G G G G − v G-v G − v vertex cut is a set of vertices U U U
s.t.
G − U is disconnected \begin{equation} G-U \text{ is disconnected} \end{equation} G − U is disconnected
这个定义在讨论,当我 cut 掉几个点,图可以从 Connected ⇒ Disconnected \text{Connected } \Rightarrow \text{ Disconnected} Connected ⇒ Disconnected
IMPORTANT
If the cardinality of vertieces in a vertex cut U U U G G G G G G G G G U U U vertex connectivity of G G G v ( G ) v(G) v ( G )
vertex conectivity : 对于G G G v ( G ) v(G) v ( G ) IMPORTANT
G G G n n n
Then, a ( G ) ≤ v ( G ) a(G) \leq v(G) a ( G ) ≤ v ( G ) G 1 ∪ G 2 G_1 \cup G_2 G 1 ∪ G 2
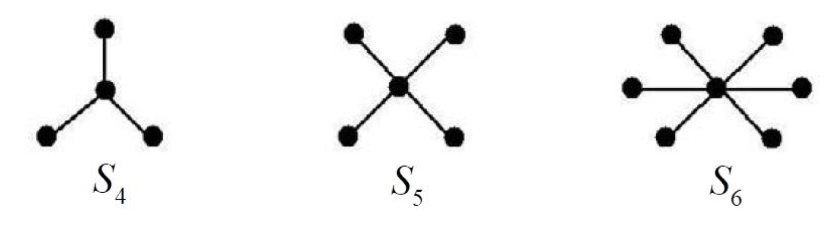
G 1 G_1 G 1 n − v ( G ) n-v(G) n − v ( G ) G 2 G_2 G 2 v ( G ) v(G) v ( G ) a ( G ) ≥ 2 v ( G ) − n a(G) \geq 2v(G) - n a ( G ) ≥ 2 v ( G ) − n KEY POINT - Star graph
A star S n S_n S n n ( ≥ 2 ) n(\geq 2) n ( ≥ 2 ) n − 1 n-1 n − 1 S n = K 1 , n − 1 S_n = K_{1,n-1} S n = K 1 , n − 1
The Laplacian eigenvalues of S n S_n S n 0 , 1 , . . . , 1 , n 0,1,...,1,n 0 , 1 , ... , 1 , n 1 1 1 n − 1 n-1 n − 1
For S 4 : 0 , 1 , 1 , 4 S_4: 0,1,1,4 S 4 : 0 , 1 , 1 , 4 For S 5 : 0 , 1 , 1 , 1 , 5 S_5: 0,1,1,1,5 S 5 : 0 , 1 , 1 , 1 , 5 For S 6 : 0 , 1 , 1 , 1 , 1 , 6 S_6: 0,1,1,1,1,6 S 6 : 0 , 1 , 1 , 1 , 1 , 6 Corollary
Let T T T n ≥ 3 n\geq 3 n ≥ 3 a ( T ) ≤ 1 a(T)\leq 1 a ( T ) ≤ 1 T T T star graph
KEY POINT - Pendant, Quasipendant
A vertex in a graoh G G G one is called a pendant vertices .
p ( G ) p(G) p ( G ) pendant vertices .A vertex in G G G quasipendant if it is adjacent to a pendant vertex.
q ( G ) q(G) q ( G ) quasipendant m G ( λ ) m_{G}(\lambda) m G ( λ ) λ \lambda λ G G G
Relationship between Pendant, Quasipendant, and the number of eigenvalue equal 1
Let L ( G ) L(G) L ( G ) G G G
m G ( 1 ) ≥ p ( G ) − q ( G ) \begin{equation} m_{G}(1) \geq p(G) - q(G) \end{equation} m G ( 1 ) ≥ p ( G ) − q ( G )
KEY POINT
Let G G G p p p R R R G G G
S ( G ) = m L [ R ] ( 1 ) = m A ( 1 ) S(G) = m_{L[R]}(1) = m_{A}(1) S ( G ) = m L [ R ] ( 1 ) = m A ( 1 )
S ( G ) = m G ( 1 ) − p ( G ) + q ( G ) S(G) = m_{G}(1) - p(G) + q(G) S ( G ) = m G ( 1 ) − p ( G ) + q ( G )
A A A
L ( G ) = [ A X 0 r , p X Q C 0 r , p C T I p ] \begin{equation} L(G) = \begin{bmatrix} A &X &0_{r,p} \\ X &Q &C \\ 0_{r,p} &C^{T} &I_{p} \\ \end{bmatrix} \end{equation} L ( G ) = A X 0 r , p X Q C T 0 r , p C I p
KEY POINT
Let G G G n n n m G ( I ) m_{G}(I) m G ( I ) L ( G ) L(G) L ( G ) I I I m G [ 0 , 1 ] ≥ p ( G ) ≤ m G [ 1 , + ∞ ] m_{G}[0,1] \geq p(G) \leq m_{G}[1, +\infty] m G [ 0 , 1 ] ≥ p ( G ) ≤ m G [ 1 , + ∞ ]
Theorem
Let G G G n n n G u v P 3 GuvP_3 G uv P 3 G + P 3 G+P_3 G + P 3 u u u G G G v v v P 3 P_3 P 3
m G ( 1 ) = m G u v P 3 ( 1 ) \begin{equation} m_G(1) = m_{GuvP_3}(1) \end{equation} m G ( 1 ) = m G uv P 3 ( 1 )
Definition
Denote by ξ ( G ) \xi(G) ξ ( G ) L ( G ) L(G) L ( G ) a ( G ) a(G) a ( G )
The element of ξ ( G ) \xi(G) ξ ( G ) characteristic valuations of G G G
Characteristic valuation
Let T = ( V , E ) T = (V,E) T = ( V , E ) n ≥ 4 n\geq 4 n ≥ 4 characteristic valuation x 2 T ∈ ξ ( T ) x_2^T \in \xi(T) x 2 T ∈ ξ ( T ) v ∈ V ( G ) v \in V(G) v ∈ V ( G ) x 2 T ( v ) = 0 x^T_2(v)=0 x 2 T ( v ) = 0 u ∈ V ( G ) u \in V(G) u ∈ V ( G ) v v v T 1 = ( V , E ) T_1 = (V,E) T 1 = ( V , E ) V V V { u , v } \{u,v\} { u , v }
Then,
(a) x 2 T ( u ) = 0 (b) a ( T 1 ) = a ( T ) (c) x 2 T ∈ ξ ( T ) , where x 2 T is the restriction of x 2 T to V 1 \begin{equation} \begin{array}{lr} \text{(a)} \quad x_2^T(u) = 0 &\\ \\ \text{(b)} \quad a(T_1) = a(T) &\\ \\ \text{(c)} \quad x^T_2 \in \xi(T),\text{ where }x^T_2 \text{ is the restriction of } x_2^T \text{ to } V_1 \end{array} \end{equation} (a) x 2 T ( u ) = 0 (b) a ( T 1 ) = a ( T ) (c) x 2 T ∈ ξ ( T ) , where x 2 T is the restriction of x 2 T to V 1